Akordiline ja mitteakordiline figuratsioon. Abiheli: ühe- ja kahepoolsed abihelid, topeltabihelikäik, apodžatuur. Läbiminev heli. Pideheli ehk pide. Ennakheli. Konsoneerivad mitteakordihelid.

Figuratsioon on kaunistamine. Kitsamalt peetakse figuratsiooni all silmas eelkõige meloodilise hääle kaunistamist ehk meloodilist figuratsiooni. Kuna meloodilise hääle moodustumine sõltub harmoonilisest taustsüsteemist, siis saab figuratsioonist rääkida kui meloodiahääle akordilisest (chordal figuration) või mitteakordilisest figuratsioonist (nonharmonic figuration) ning selle tulemusena tekkivatest meloodilistest figuratsioonihelidest kui akordi- või mitteakordihelidest.

Meloodiahääle akordiline figuratsioon tekib akordiheli kaunistamisel teiste samasse akordi kuuluvate helidega. Mainitud nähtust nimetatakse ka arpedžeerimiseks ehk liikumiseks hetkel kõlava akordi helidel. Meloodiahääle akordilise figuratsiooniga kaasnevad meloodilises hääles üldreeglina hüpped, s.t meloodilised tertsid või sellest suuremad intervallid. Meloodiahääle figureerimisel konsoneeriva akordi helidega tekivad nn konsoneerivad helid, sest nende ja ülehäänud häälte vahel moodustuvad vaid konsoneerivad intervallid. Meloodiahääle akordilisel figureerimisel tekib ka nähtus, milles meloodiahääl moodustub kahest või enamast mõttelisest häälest. Seda nähtust nimetatakse varjatud mitmehäälsuseks.

Näide I.8.1, Akordiline figuratsioon

Kommentaar: Kaunistamata (figureerimata) akordijärgnevus I-V₄₃-I (a) ja selle kaunistatud (figureeritud) variandid (b–d).

Näide I.8.2, Meloodiahääle akordiline figuratsioon kui mõtteline liikumine kahe hääle vahel

Kommentaar: a) kolmehäälne helijärgnevus ja b) kahehäälne helijärgnevus, mille ülemine hääl moodustub liikumisest kahe mõttelise hääle (näite a kahe ülemise hääle) vahel.

Meloodiahääle mitteakordilise figuratsiooni tulemusena moodustuvad mitteakordihelid liigitatakse abihelideks, läbiminevateks helideks, pidehelideks ja ennakhelideks. Abiheli tekib (akordi)heli kaunistamisel naaberastmel kõlava heliga. NB! Abihelile liikumine ja sellelt ära liikumine on alati vastassuunalised; s.t kui abihelile liigutakse tõusvalt (moodustub ülemine abiheli), siis sellelt ära liigutakse laskuvalt ning kui abihelile liigutakse laskuvalt (moodustub alumine abiheli), siis sellelt ära liigutakse tõusvalt. Abiheli võib olla ühtlasi ühe- või kahepoolne. Kahepoolse abiheli puhul tekib abiheli kahe sama heli (astme) vahel, ühepoolse abiheli puhul aga kahe erineva heli vahel. Viimasel juhul on abiheli astmeliselt seotud ainult ühe heliga (s.t heliga, mida ühepoolne abiheli kaunistab).

Abiheli moodustub üldreeglina meetrumi suhteliselt rõhutul osal (s.t rõhutumal osal võrreldes heliga, mida abiheli kaunistab). Meetrumi suhteliselt rõhutul osal kõlavad ühepoolsed abihelid võivad moodustuda kolmel viisil: (1) abihelidena, millelt lahkutakse hüppega, (2) abihelidena, millele liigutakse hüppega ning (3) topeltabihelikäiguna. Esimesel juhul kaunistab abiheli eelnevat heli, teisel juhul järgnevat heli ning kolmandal juhul on mingi heli kaunistatud nii ülemise kui ka alumise abiheliga (vastupidine abihelide järjekord on haruldane). Mõnikord võivad kahepoolsed abihelid moodustuda ka meetrumi rõhulisel osal. Kui meetrumi rõhulisel osal moodustub ühepoolne abiheli, liigutakse sellele alati hüppega ning see laheneb astmeliselt hüppele vastupidises suunas. Sellist figuratsiooni tüüpi nimetatakse ka apodžatuuriks.

Näide I.8.3, Abihelid

Kommentaar: a) ülemine kahepoolne abiheli, b) alumine kahepoolne abiheli, c) ühepoolne abiheli, millelt lahkutakse hüppega, d) ühepoolne abiheli, millele liigutakse hüppega, e) topeltabihelikäik ning f) apodžatuur (rõhuline ühepoolne abiheli, millele liigutakse hüppega, vt ka näidet I.8.5c).

Läbiminev heli tekib astmelisel ja ühesuunalisel liikumisel ühelt akordihelilt teisele, kusjuures liikumine võib olla nii tõusva- kui ka laskuvasuunaline. Ühtlasi on läbiminev heli alati astmeliselt seotud nii eelneva kui ka järgneva heliga. Läbiminev heli tekib samuti reeglina meetrumi suhteliselt rõhutul osal, kuid mõnikord siiski ka rõhulisel osal. Rõhulist läbiminevat heli eristab apodžatuurist helile eelneva hüppe puudumine, viimast asendab astmeliselt laskuv või tõusev liikumine.

Näide I.8.4, Läbiminevad helid

Kommentaar: a) läbiminev heli, mis tekib tõusval liikumisel, b) läbiminev heli, mis tekib laskuval liikumisel ning c) rõhulisel meetrumiosal moodustuv läbiminev heli.

Pideheli ehk pide on mitteakordiheli, mis tekib eelneva akordi heli üleviimisel järgnevasse akordi. Pide kui kaunistusvõte koosneb kolmest komponendist: (1) pideheli ettevalmistusest, milles pideks muutuv heli moodustab konsoneerivaid intervalle kõigi ülejäänud harmoonia helidega, (2) pidest endast, milles eelmisest akordist kinnipeetud konsoneeriv akordiheli muutub uue akordi saabumisega dissoneerivaks mitteakordiheliks ehk pideks, ning (3) pide lahendusest, milles dissoneeriv pideheli laheneb astmeliselt laskuvalt uue akordi konsoneerivasse helisse. Erinevalt eelpool käsitletud mitteakordilistest figuratsioonihelidest kõlab pide võrreldes ettevalmistuse ja lahendusega alati meetrumi suhteliselt rõhulisel osal. Mõnikord võib pideks muutuval helil samas hääles ettevalmistus puududa. Sellist figuratsioonitüüpi käsitletakse ettevalmistamata pidena ning oma avaldusvormi tõttu võib seda käsitleda nagu rõhulist ühepoolset abiheligi (vt näide I.8.3f) apodžatuurina.

Näide I.8.5, Pide

Kommentaar: a) pide ja selle erinevad komponendid: 1) ettevalmistus, 2) pide ja 3) lahendus, b) pide keskmises hääles, c) ettevalmistamata pide ehk apodžatuur (vt ka näidet I.8.3f).

Ennakheli ehk ennak on mitteakordiheli, mis tekib järgneva akordi heli ennetamisel. Kui pide kõlab alati meetrumi rõhulisel, siis ennak alati meetrumi rõhutul osal. Kuigi ennakhelile liigutakse sageli astmeliselt, ei ole võimatu ka hüppeline liikumine.

Näide I.8.6, Ennak

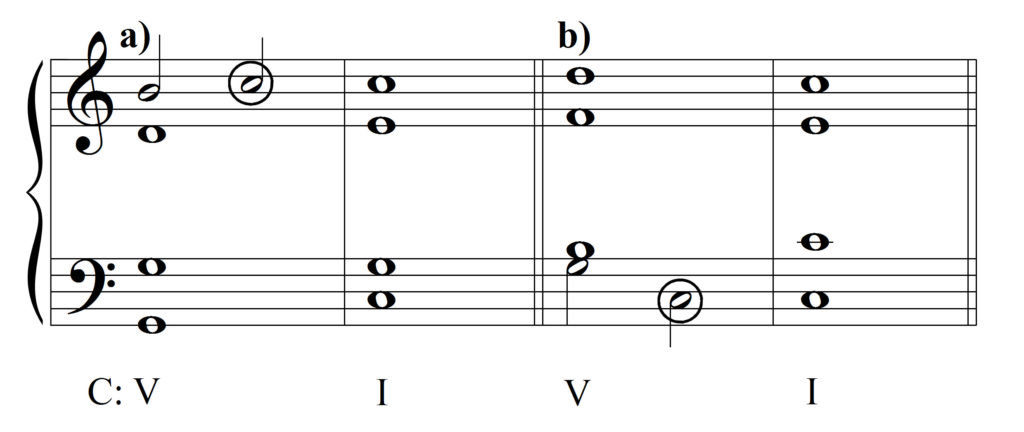
Kommentaar: a) ennakheli ülahääles, millele liigutakse astmeliselt, b) ennakheli alumises hääles, millele liigutakse hüppega.

Kuigi mitteakordilise figuratsiooni tulemusena tekkivad mitteakordihelid on üldreeglina dissoneerivad helid (s.t et need moodustavad ühe või enama akordiheliga dissoneerivaid intervalle), on mõnikord võimalikud ka konsoneerivad mitteakordihelid. Nende eristamiseks tavapärastest dissoneerivatest mitteakordihelidest kasutatakse ka konsoneeriva abiheli, konsoneeriva läbimineva heli, konsoneeriva pide ja konsoneeriva ennakheli mõisteid.

Näide I.8.7, Konsoneerivad mitteakordihelid

Kommentaar: a) konsoneeriv abiheli, b) konsoneeriv läbiminev heli, c) konsoneeriv pide, d) konsoneeriv ennakheli.