V.5 Modulatsioon kaugsugulushelistikku. Järk-järguline modulatsioon kaugsugulushelistikku. Järsk modulatsioon kaugsugulushelistikku: harmooniliselt kaugete tertsisuhteliste helistike ühendamine. Enharmooniline modulatsioon vähendatud septakordi ja väikse mažoorse septakordi enharmoonilise ümbermõtestamise kaudu. Sümmeetriline harmoonia ja oktavi jagamine võrdseteks osadeks.

Modulatsiooniks kaugsugulushelistikku nimetatakse üleminekut ühest helistikust teise, mille puhul alg- ja sihthelistik erinevad teineteisest vähemalt kahe võtmemärgi võrra. Modulatsioon kaugsugulushelistikku võib toimuda järk-järgult või järsku. Järk-järgulise kaugmodulatsiooni puhul kasutatakse kaugsuguluses alg- ja lõpphelistiku ühendamiseks vahehelistikke nii, et kõrvutiasetsevad ehk üksteisega vahetult kokku puutuvad helistikud on lähisuguluses. Näiteks C-duuri (võtmemärgid puuduvad) ühendamiseks D-duuriga (võtmemärkideks on kaks dieesi) kasutatakse vahehelistikuna G-duuri või e-molli (võtmemärgiks on üks diees). Selle tulemusena moodustuvas helistikejärgnevuses C-duur, G-duur, D-duur või C-duur, e-moll, D-duur on kõik kõrvutiasetsevad helistikud lähisuguluses. Kui aga C-duuri soovitakse ühendada näiteks Es-duuriga (võtmemärkideks on kolm bemolli), siis tuleks kasutada juba kahte vahehelistikku: esimeseks vahehelistikuks saab olla kas F-duur või d-moll (võtmemärgiks on üks bemoll) ning teiseks vahehelistikuks B-duur või g-moll (võtmemärgiks on kaks bemolli). Seega, mida suurem on erinevus alg- ja lõpphelistiku võtmemärkide osas, seda suurem on ka vastavaid helistikke ühendavate vahehelistike arv.

Kõrvutiasetsevaid helistikke ühendades kasutatakse modulatsioonitehnikat, mida kirjeldati juba lähimodulatsiooni peatükis (vt ptk V.3), s.t modulatsiooni ühise akordi kaudu: esmalt leitakse kahte helistikku ühendav akord, millel tehakse võrrutamine (akordi ümbermõtestamine uue helistiku kontekstis), sellele järgneb moduleeriv akord (keerukam predominant- või dominantakord uues helistikus) ning sellele omakorda viimase lahendusakord (tavaliselt uue helistiku toonikaakord). Järgnevatesse helistikesse moduleerimisel läbitakse sama protseduur nii mitu korda, kuni jõutakse lõpphelistikuni. Nii näiteks võib järk-järgulise modulatsiooni C-duurist D-duuri (e-molli kaudu) vormistada järgnevalt: C: I = e: VI-II₆₅-V₂-I₆ = D: II₆-K₆₄-V₇-I (vt näite V.5.1 takte 5–8).

Näide V.5.1, Järk-järguline modulatsioon kaugsugulushelistikku

Järsu kaugmodulatsiooni puhul ühendatakse kaks kaugsuguluses olevat helistikku otse, s.t ilma vahehelistiku või vahehelistiketa. Olenevalt helistike sugulusastmest (võtmemärkide erinevuse määrast) leidub selleks erinevaid võimalusi. Kahe võtmemärgi võrra erinevaid helistikke saab nagu lähisugulushelistikke ühendada ühise akordi abil, kuigi vastavaks akordiks ei saa olla enam alg- või lõpphelistiku toonikakolmkõla. Näiteks C-duuri saab D-duuriga ühendada G-duur või e-moll kolmkõla kaudu: alghelistikus funktsioneerivad need V või III astme kolmkõla, lõpphelistikus aga IV või II kolmkõlana. Analoogiliselt saaks C-duuri ühendada B-duuriga kas F-duur või d-moll kolmkõla kaudu: alghelistikus funktsioneeriks mainitud kolmkõlad kas IV või II ning lõpphelistikus kas V või III kolmkõlana. Sarnaselt oleks ühendamine võimalik ka siis, kui üks või mõlemad ühendatavatest helistikest oleksid minoorhelistikud: a-mollist D-duuri liikudes võrrutataks loomulik VII või V astme kolmkõla IV või II kolmkõlaga (h-molli liikudes VI või IV kolmkõlaga) ning a-mollist B-duuri liikudes VI või IV kolmkõla V või III kolmkõlaga (g-molli liikudes loomuliku VII või V kolmkõlaga). Kui kalduvaid sekventse mitte arvestada (näiteks C: V₆₅/V-V-V₆₅/IV-IV), esineb kahe võtmemärgi kaugusel olevate helistike otsest ühendamist (või kõrvutamist) tonaalses muusikas siiski suhteliselt harva, sest hoolimata kaugsugulusest pole kõlaline kontrast nende puhul veel piisavalt suur – viimane on aga see, mida järsu modulatsiooni puhul üldreeglina taotletakse (vt näide V.5.2).

Näide V.5.2, Järsk modulatsioon kahe võtmemärgi kaugusel olevasse helistikku

Seetõttu on tavapärasem kahe sellise kaugsuguluses oleva helistiku ühendamine, kus sihthelistiku toonikaakord või selle mõni muu tavapärane akord on alghelistikus laadilise segunemise tulemusel moodustuv akord. Kuna laadiline segunemine on tavalisem mažoori puhul, siis on ka laadilisel segunemisel põhinev järsk modulatsioon omane pigem mažoorsetele helistikele. Teatavasti on tüüpilised laadilise segunemisega seonduvad kolmkõlad mažooris harmooniline subdominant (_hIV ehk IV^b3), samuti toonikakolmkõla madala tertsiga (I^b3) ning ülemise ja alumise mediandi mitmesugused kõrgendatud ja madaldatud variandid (III^b1,5 ja VI^b1,5 kui otsese laadilise segunemise ning III^#3 ja VI^#3 kui kaudse laadilise segunemise tulemusena moodustuvad akordid; vt ptk V.2). Seega oleks näiteks C-duurist võimalik moduleerida f-molli (= C: _hIV ehk IV^b3), c-molli (= C: I^b3), Es-duuri (= C: III^b1,5), As-duuri (= C: VI^b1,5), E-duuri (= C: III^#3) ja A-duuri (= C: VI^#3) ning kõikide nimetatud helistike lähisugulushelistikesse. Minooris on laadilise segunemise üheks tüüpilisemaks avaldumisvormiks aga toonikakolmkõla kõrgendatud tertsiga (I^#3; vt ptk V.2). Seega oleks näiteks c-mollist võimalik moduleerida C-duuri (= c: I^#3) ning nimetatud mažoori lähisugulushelistikesse.

Kuigi nõnda moodustuvate võimalike sihthelistike ring on üsna lai, kasutatakse laadilisel segunemisel põhinevat järsku modulatsiooni eelkõige harmooniliselt kaugete tertsisuhteliste helistike ühendamiseks ehk liikumiseks helistikesse, mille toonikakolmkõla mažoorses alghelistikus on juba mainitud III^b1,5, VI^b1,5, III^#3 ja VI^#3 ja minoorses alghelistikus tavaliselt VI^#1,5. Modulatsiooniprotsess avaldub tavaliselt kolmel viisil: kas 1) kahe samanimelise helistiku toonikakolmkõla vastandamise, 2) kahte ühist heli omava tertsisuhtelise kolmkõla vastandamise või 3) kahte helistiku ühendava ühise akordi kaudu, mille puhul võrrutatav akord on alghelistikus laadilise segunemise tulemusel moodustuv akord.

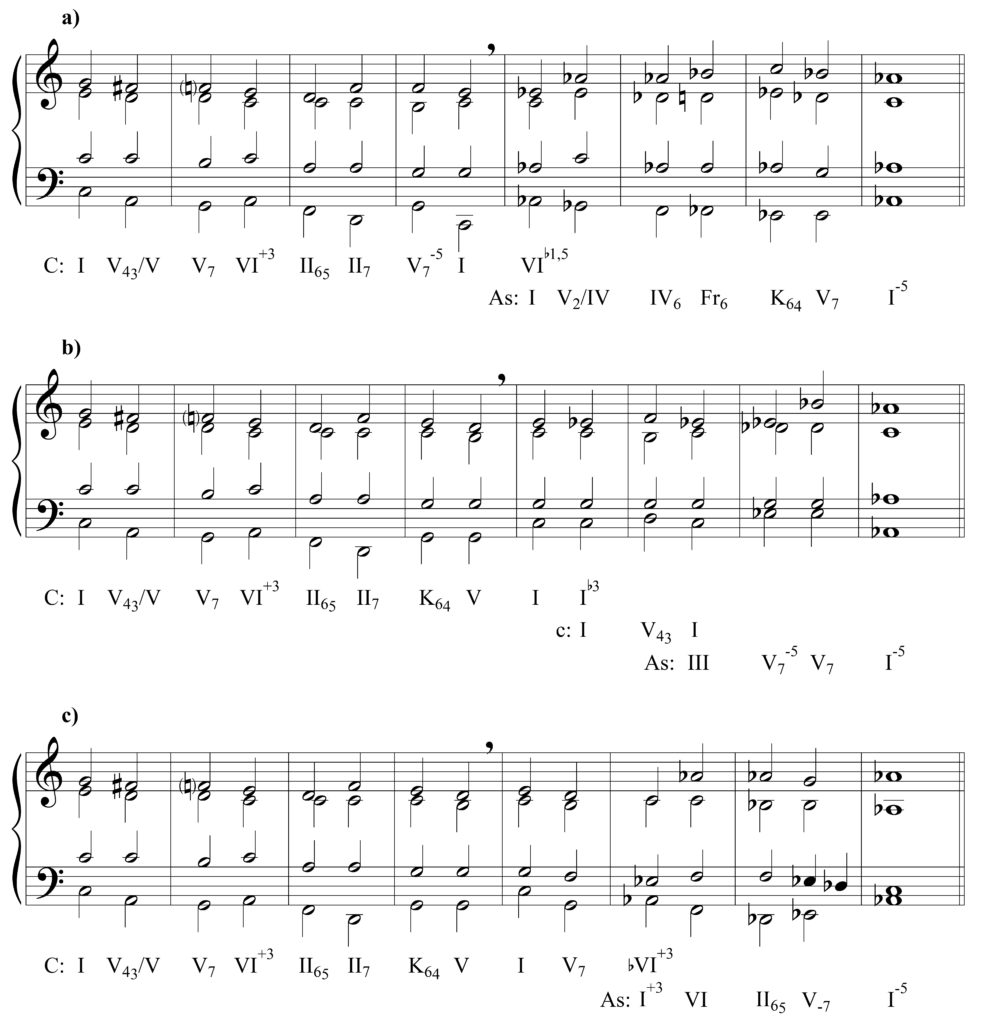
Näiteks kasutatakse kahe samanimelise helistiku toonikakolmkõla vastandamist madaldatud kolmanda astme kolmkõlasse (III^b1,5) moduleerimiseks. Sellise modulatsiooni esimeses etapis vastandatakse mingi mažoorse helistiku toonikakolmkõla samanimelise minoorse helistiku toonikakolmkõlaga, kusjuures on üsna tavaline, et mainitud vastandamise vahele jääb vormiosasid eraldav tsesuur. Järgmises etapis võrrutatakse minoorne toonikakolmkõla selle paralleelhelistiku VI astme kolmkõlaga, millele viimases etapis järgneb omakorda kadents mainitud minoorhelistiku paralleelhelistikus. Sellise modulatsiooni võimalik akordiplaan võiks olla järgmine: C: I ’ I^b3 = c: I = Es: VI-IV-K₆₄-V₇-I (= C: III^b1,5; vt näide V.5.3a, modulatsioonivariant 1).

Mõnikord võib alghelistiku madaldatud tertsiga (ehk samanimelise minoori) toonikakolmkõlasse liikuda ka samanimelisi helistikke ühendava ühise dominandi kaudu (vt näite V.5.3a neljanda takti alternatiivset varianti, mis on ära toodud süsteemi a all). Ühtlasi võib alghelistikuga samanimeline minoor kui vahehelistik olla siin ka täiendavalt lahti komponeeritud, nagu näiteks: C: I-V₇ ’ I^b3 = c: I-Ger₆-V-III = C: I-II₆₅-V_-7-I (= C: III^b1,5; vt näide V.5.3b). Alati ei pea aga kahte helistikku ühendavaks akordiks olema alghelistiku I^b3, vaid selleks võib olla ka mõni muu alghelistiku laadilise segunemise tulemusel moodustuv akord, näiteks mažooris VI^b1,5, mille esimene pööre ühendab näites V.5.3c C-duuri Es-duuriga: C: I-VI₆^b1,5 = Es: IV₆-I₆₄-Ger₆-K₆₄-V-I (= C: III^b1,5; modulatsioonivariant 3) Erinevalt eelpool toodud näidetest avaldub selline modulatsioon aga vormiliselt ühe lause sees ehk mitte üle tsesuuri (s.t kahe lause ühendamisel nagu enamikes eelpool toodud näidetes).

Näide V.5.3, Laadilisel segunemisel põhinev järsk modulatsioon (I): modulatsioon duuris bIII astmesse

Madala VI astme helistikku (VI^b1,5) liikumiseks kasutatakse samuti sageli lihtsalt helistike vastandamist (modulatsioonivariant 2), mis toimub alati üle tsesuuri ehk üle vormilise liigenduskoha (vt näide V.5.4a). Teiseks võimaluseks on moduleerida mažoorsest alghelistikust ühise dominandi kaudu samanimelisse minoori (nagu see toimub ka moduleerimisel madala kolmanda astme helistikku), mille toonikakolmkõla võrrutatakse seejärel sihthelistiku III astme kolmkõlaga; võrrutamisele järgneb omakorda kadents sihthelistikus (modulatsioonivariandi 1 arendatud kuju; vt näide V.5.4b). Kolmanda võimalusena saab alghelistikust liikuda kohe madala VI astme kolmkõlasse ja see siis täiendava kadentsi abil muuta uue helistiku toonikaks (modulatsioonivariant 3; vt näide V.5.4c).

Näide V.5.4, Laadilisel segunemisel põhinev järsk modulatsioon (II): modulatsioon duuris bVI astmesse

Ka mažoorsesse kolmanda astme (III^#3) helistikku liigutakse üldreeglina helistike lihtsa vastandamise kaudu (modulatsioonivariant 2). Nagu kõikide vastandamiste puhul, toimub ka see tavaliselt vormilistes liigenduskohtades (vt näide V.5.5a). Moduleerimisel mažoorsesse kuuenda astme (VI^#3) helistikku saab III^#3 kasutada ka sihthelistiku dominandina (modulatsioonivariant 2; vt näide V.5.5b). Kõrge kuuenda astme helistikku saab moduleerida ka mollhelistikust, mida tehakse siis aga alghelistiku toonikakolmkõla ja selle kõrge tertsiga variandi vastandamise kaudu (modulatsioonivariant 1; vt näide V.5.5c).

Näide V.5.5, Laadilisel segunemisel põhinev järsk modulatsioon (II): modulatsioon duuris III^#3 ja VI^#3 ning mollis #VI astmetesse

Enharmooniliseks modulatsiooniks nimetatakse modulatsiooni enharmooniliselt ümbermõtestatava akordi abil. Harmoonias eristatakse n-ö näilist enharmonismi tegelikust ehk sisulisest enharmonismist. Esimesel puhul kasutatakse enharmonismi lihtsalt noodikirja parema ülevaatlikkuse huvides, näiteks siis kui As-duuri madala kuuenda astme helistik või Des-duuri madala kolmanda astme helistik Fes-duur kirjutatakse üles viimasega enharmoonilise helistiku E-duurina. Tegeliku ehk sisulise enharmonismi puhul muutub aga akordi ümbermõtestamisel mitte ainult selle helistikuline kuuluvus, vaid ka selle funktsioon (tavaliselt dominant predominandiks, harvem ka vastupidi), kusjuures akordihelide enharmooniline ümbermõtestamine ei pruugi noodikirjas alati kajastuda.

Enharmoonilisele modulatsioonile iseloomulik efekt avaldub eelkõige just harmooniliselt kaugetesse helistikesse moduleerimisel. Akord, millel enharmooniline ümbermõtestamine toimub, on tavaliselt kas vähendatud septakord (või selle pööre) või väike mažoorne septakord. Esimesel juhul mõtestatakse alghelistiku või selle lähisugulushelistikku juhtseptakord (või selle pööre) ümber sihthelistiku kõrgendatud neljandalt või (minooris ka kõrgendatud) kuuendalt astmelt üles ehitatud dominandi dominandi juhtseptakordi või selle esimese pöördega, näiteks C: >VII₄₃ = gis: >VII₆₅/V või C: >VII₇/III = Fis: >VII₆₅/V (tüüp 1; vt näiteid V.5.6a ja b). Samuti saab alghelistiku vähendatud juhtseptakordi või selle pöörde võrrutada enharmooniliselt kohe lõpphelistiku vähendatud seitsmenda astme sekundakordiga (tüüp 2). Enharmoonilisena saab modulatsiooni mõista siis, kui vähemalt üks võrrutatava akordi helidest asendatakse võrrutamise käigus vastava heli enharmoonilise ekvivalendiga. Esimena toodud näites asendatakse alghelistiku helid as, d ja f sihthelistiku enharmooniliste helidega gis, cisis ja eis (vt näide V.5.6a), teisena toodud näiteks aga alghelistiku heli c sihthelistiku heliga his (vt näide V.5.6b).

Näide V.5.6, Enharmooniline modulatsioon (I): alghelistiku (kõrvalastme) juhtseptakordi või selle pöörde enharmooniline ümbermõtestamine sihthelistiku predominandiks >VII₆₅/V

Teisel juhul mõtestatakse aga alghelistiku või selle lähisugulushelistikku dominantseptakord ümber sihthelistiku saksa sekstiks, näiteks C: V₇ = H: Ger₆ või C: V₇/IV = E: Ger₆. Esimesel juhul asendatakse alghelistiku helid d ja f sihthelistikus enharmooniliste helidega cisis ja eis (juhul kui Ger₆ kirjutatakse sihthelistikus ehk H-duuris akordina _hII₄₃^#1,3; vt näide V.5.7a) või ainult heli f heliga eis (juhul kui Ger₆ kirjutatakse sihthelistikus akordina _hIV₆₅^#1,b3), teisel juhul aga alghelistiku helid g ja b sihthelistiku helidega fisis ja ais (juhul kui Ger₆ kirjutatakse sihthelistikus ehk E-duuris akordina _hII₄₃^#1,3) või ainult heli b heliga ais (juhul kui Ger₆ kirjutatakse sihthelistikus akordina _hIV₆₅^#1,b3).

Näide V.5.7, Enharmooniline modulatsioon (II): alghelistiku (kõrvalastme) dominantseptakordi enharmooniline ümbermõtestamine sihthelistiku saksa sekstiks (Ger₆)

Nagu näited V.5.6 ja V.5.7 demonstreerivad, järgneb mõlemal juhul akordi enharmoonilisele ümbermõtestamisele selle lahenemine sihthelistiku dominanti, mis on sageli omakorda figureeritud V astme kolmkõlale või septakordile eelneva kadentsikvartsekstakordiga. Mainitud modulatsioon võib avalduda ka ümberpöördult, kus alghelistiku saksa sekst võrrutatakse enharmooniliselt sihthelistiku dominantseptakordiga, näiteks C: I-IV₆-Ger₆ = Des: V₇-I-V₇-I (vt näide V.5.8).

Näide V.5.8, Enharmooniline modulatsioon (III): alghelistiku saksa seksti (Ger₆) enharmooniline ümbermõtestamine sihthelistiku dominantseptakordiks (V₇)

Harmoonia kromatiseerumisega kaasneb nähtus, mida nimetatakse n-ö sümmeetriliseks harmooniaks. Tavapärases heptatoonikas jagatakse oktav seitsmeks osaks (astmeks), kuid nimetatud osad ehk intervallid heptatoonilise laadi astmete vahel pole võrdse suurusega: kui näiteks loomuliku mažoori 3. ja 4. ja 7. ja 8. (1.) astme vahel moodustuvad pooltoonid (väiksed sekundid), siis mainitud laadi ülejäänud naaberastmete vahel täistoonid (suured sekundid). Seetõttu võib sellist jagamist nimetada ka oktavi asümmeetriliseks jaotuseks.

Sümmeetriline harmoonia põhineb aga oktavi (või selle osa) jagamisel rangelt võrdseteks intervallideks, milleks võivad olla kas v2. s2, v3 või s3 (teataval juhul ka tritoon; ülejäänud intervalle oktavi võrdseks jagamiseks kasutada ei ole võimalik). Erinevalt heptatoonikast, kus mõni eelnevalt mainitud intervall võib sõltuvalt seotusest konkreetsete laadi astmetega avalduda nii väikse kui ka suurena (sellist intervalli nimetatakse ka diatooniliseks intervalliks), moodustuvad oktavi võrdsest jagamisest tuletatud sümmeetrilises helireas või -koosluses ainult täpselt ühesugused intervallid. Kromaatilises harmoonias asendavad sellised ühesugused intervallid mõnikord diatoonilisi intervalle ja seda eelkõige harmoonilistes sekventsides.

Näiteks võib rangelt kromaatilinse sekvents avalduda järgnevusena, milles iga järgnev lüli on transponeeritud pooltooni võrra kõrgemale (sümmeetriline sekundisuhteline sekvents). Sellises sekventsis järjestatakse näiteks c-moll, cis-moll ja d-moll kolmkõlad, mis on kõik neile eelnevate kõrvaldominantide abil tonikaliseeritud: C: I^5-b6 = Des: V₆-I^5-b6 = D: V₆-I jne (vt näide V.5.9b). Antud järgnevus on tuletatud küll tõusva sekundisuhtelise sekventsi mudelist 5-6-5-6 (vt näide V.5.9a), kuid tervikuna pole see kui sekvents enam diatoonikale taandatav, sest sekventsi iga järgnev lüli ei tonikaliseeri siin diatoonilise helirea järgmist astet, vaid pooltooni võrra kõrgemal asuvat kolmkõla.

Näide V.5.9, Sümmeetriline kromaatiliselt tõusev sekundisuhteline sekvents

Sümmeetriline sekundisuhteline sekvents võib aga avalduda ka kujul, kus sekventsi iga järgnev lüli kõlab täistooni võrra kõrgemalt või madalamalt. Nagu sekundisuhtelisele sekventsile omane, võib see avalduda paralleelsete sekstakordide järgnevusena (vrd näiteid V.5.10a ja b; näites a on V₆ prolongeeritud diatoonilise ja näites b täistooniliselt liikuva sümmeetrilise sekventsi abil). Täistooniliselt liikuvas sekventsis võivad harmooniad olla eelnevate kõrvaldominantide kaudu ka tonikaliseeritud (vt näidet V.5.10c, milles täistooniliselt tõusev sekvents ühendab toonikat madala VI astme kolmkõlaga).

Näide V.5.10, Sümmeetriline täistooniliselt liikuv sekundisuhteline sekvents

Üheks kõige tüüpilisemaks sümmeetrilise harmoonia avaldusvormiks on oktavi jagamine neljaks väikseks tertsiks. Elementaarkujul avaldub selline järgnevus üksteisest väikse tertsi kaugusel olevate kolmkõlade sekventsjärgnevusena (vt näide V.5.11a). Samas võivad mainitud kolmkõlad olla ka eelnevate kõrvaldominantide abil tonikaliseeritud (vt näide V.5.11b; ülevaatlikkuse huvides on tonikaliseeritud kolmkõlad toodud rasvases kirjas).

Näide V.5.11, Sümmeetriline tertsisuhteline sekvents

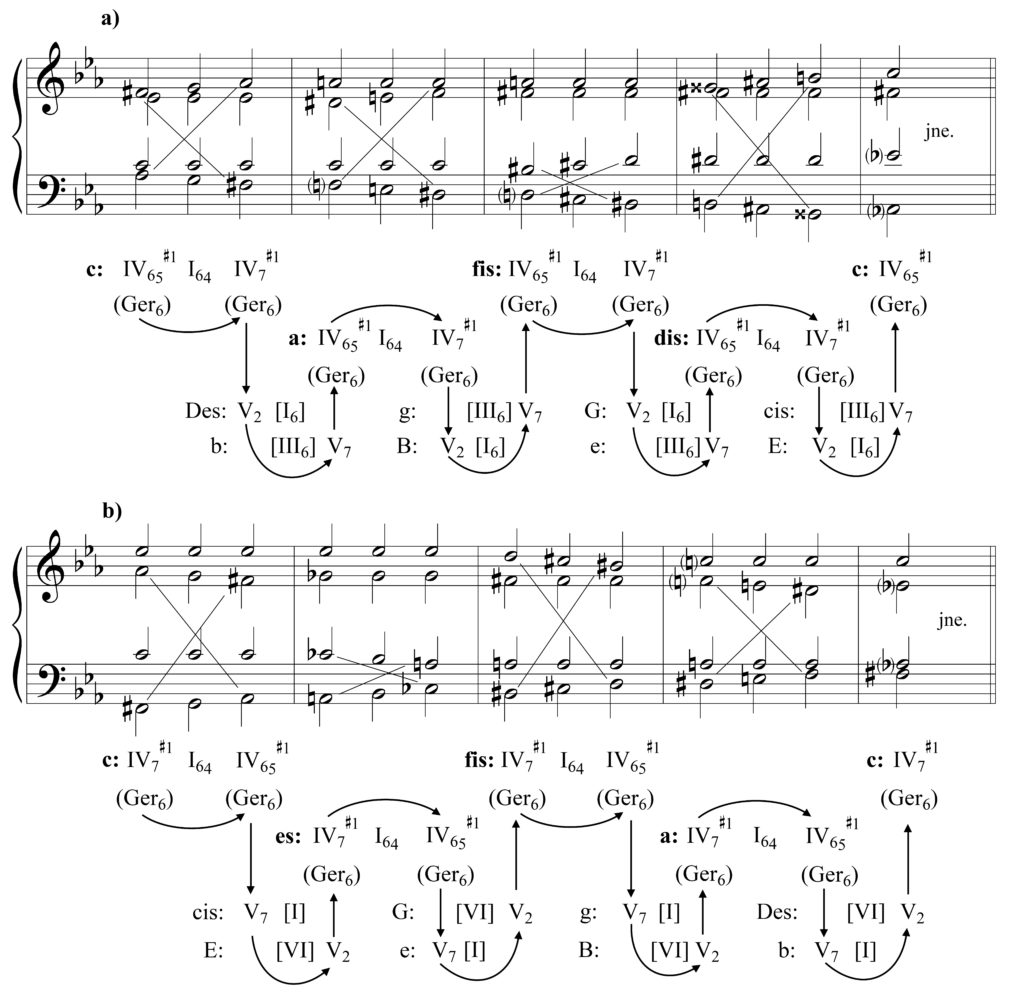
Üheks tuntuimaks sümmeetriliseks tertsisuhteliseks järgnevuseks on aga nn omnibus. Tegemist on sekventsjärgnevusega, mille iga lüli moodustub kahe kromaatiliselt ja vastassuunaliselt liikuva tertsikäigu ühendamise tulemusena, kusjuures mainitud tertsikäikude vahel toimub ka häältevahetus (näiteks liikumisele mõnes ülahääles fis–g–as vastab bassis as–g–fis). Kahe sellise hääle ühendamisel tekib esimese harmoonilise intervallina suurendatud sekst, mis harmoniseeritakse saksa sekstiga (Ger₆ = mollis IV₆₅^#1), sellele järgnev oktav läbimineva kvartsekstakordiga (I₆₄) ning viimane intervall, vähendatud terts, saksa seksti variandiga, mis ehitatakse üles laadi  astmelt (mollis IV₇^#1; vt ptk V.1). Selle tulemusena moodustub järgnevus (mollis) IV₆₅^#1-I₆₄-IV₇^#1. Bassi tõusvasuunalisel kromaatilisel liikumisel on akordid järjestatud vastupidi: IV₇^#1-I₆₄-IV₆₅^#1.

Mainitud kolmest akordist koosnevad järgnevused, mis omnibus-tüüpi sekventsis esindavad sekventsi lülisid, ühendatakse nii, et bassi laskuval liikumisel kõlab iga lüli väikse tertsi võrra madalamalt, tõusva liikumise puhul aga väikse tertsi võrra kõrgemalt. Harmoonilises plaanis saab mehhanismi, mille kaudu omnibus-tüüpi sekventsis ühendatakse selle lüli järgnevaga mõista omalaadse kombinatsioonina enharmoonilisest modulatsioonist ja ellipsjärgnevusest: esmalt mõtestatakse lüli viimane akord (saksa sekst või selle variant) uues helistikus enharmooniliselt ümber dominantseptakordiks või -sekundakordiks, millele järgneb mõni selle lähisugulushelistikku dominantseptakord või -sekundakord (järgmise sekventsilüli esimene akord), misjärel viimane mõtestatakse uues helistikus taas enharmooniliselt ümber saksa sekstiks või selle variandiks.

Näiteks bassihelilt as alguse saavas laskuvas omnibus-tüüpi järgnevuses mõtestatakse c: IV₇^#1 ümber akordiks Des: V₂, mis ei lahene aga toonikasse, vaid liigub edasi paralleelhelistiku dominantseptakordi Des: V₇/VI = b: V₇. Mainitud akord võrrutatakse enharmooniliselt sellest väikse sekundi võrra madalamal asuva helistiku saksa sekstiga (b: V₇ = a: Ger₆ ehk IV₆₅^#1). Viimane on ühtlasi uue sekventsilüli esimene akord ning peale järgnevuse a: IV₆₅^#1-I₆₄-IV₇^#1 läbiviimist kordub järgnevasse, väikse tertsi võrra madalamasse lülisse üleminekul kogu eelnevalt kirjeldatud protsess uuesti. Seega võiks täielik, s.t kogu oktavit hõlmav ja bassihelilt as alguse saav laskuvasuunaline omnibus avalduda järgnevalt (iga järgneva sekventsilüli esimene harmoonia on ülevaatlikkuse suurendamiseks antud edasi rasvases kirjas): c: IV₆₅^#1(Ger₆)-I₆₄– IV₇^#1 = Des: V₂-V₇/VI = a: IV₆₅^#1(Ger₆)-I₆₄– IV₇^#1 = B: V₂-V₇/VI = fis: IV₆₅^#1(Ger₆)-I₆₄– IV₇^#1 = G: V₂-V₇/VI = dis/es: IV₆₅^#1(Ger₆)-I₆₄– IV₇^#1 = E: V₂-V₇/VI = c: IV₆₅^#1(Ger₆) (vt näide V.5.12a).

Tõusva omnibus-tüüpi järgnevuse puhul mõtestatakse näiteks bassihelilt fis alguse saava sekventsilüli (IV₇^#1-I₆₄-IV₆₅^#1) viimane akord c: IV₆₅^#1 enharmooniliselt ümber vastavast minoorist pooltooni võrra kõrgemal asuva minoori dominantseptakordiga cis: V₇, mis seejärel ühendatakse elliptiliselt selle paralleelhelistiku dominantsekundakordiga cis: V₂/III = E: V₂. Analoogiliselt eelmise näitega võrrutatakse viimane omakorda enharmooniliselt sellest pool tooni madalamal asuva minoori 4. astmelt üles ehitatud saksa seksti variandiga dis/es: IV₇^#1. Saadud akord on ühtlasi järgmise sekventsilüli dis/es: IV₇^#1-I₆₄-IV₆₅^#1 esimene akord ning peale lüli aluseks oleva akordijärgnevuse läbiviimist kordub järgnevasse, väikse tertsi võrra kõrgemal asuvasse lülisse üleminekul kogu eelnevalt kirjeldatud protsess uuesti. Seega võiks täielik, s.t kogu oktavit hõlmav ja bassihelilt fis alguse saav tõusvasuunaline omnibus avalduda järgnevalt (iga järgneva sekventsilüli esimene harmoonia on ülevaatlikkuse suurendamiseks antud edasi rasvases kirjas): c: IV₇^#1-I₆₄-IV₆₅^#1(Ger₆) = cis: V₇-V₂/III = dis/es: IV₇^#1-I₆₄-IV₆₅^#1(Ger₆) = e: V₇-V₂/III = fis: IV₇^#1-I₆₄-IV₆₅^#1(Ger₆) = g: V₇-V₂/III = a: IV₇^#1-I₆₄-IV₆₅^#1(Ger₆) = b: V₇-V₂/III = c: IV₇^#1.

Näide V.5.12, Laskuva- ja tõusvasuunaline omnibus

Analoogiliselt diatooniliste järgnevustega avalduvad ka oktavi võrdsel jagamisel põhinevad tertsisuhtelised järgnevused sagedamini laskuvasuunalistena. Viimane on tavapärane ka oktavi jagamisel suurteks tertsideks (vt näide V.5.13).

Näide V.5.13, Oktavi jagamine suurteks tertsideks (laskuv tertsisuhteline sekvents)